8000 Tonnen Weihnachtsmüll: Wie Sie Ihre Geschenke sparsamer verpacken

8000 Tonnen. Allein in Deutschland. Das ist die geschätzte Masse zusätzlichen Verpackungsmülls, die uns das Christkind und der Weihnachtsmann jährlich bescheren: Pappe, Papier, Kunststoff.

Muss das sein? Warum verpacken wir Geschenke überhaupt? Denn noch kein Geschenk dieser Welt hat jemals in seiner Verpackung seinen Zweck erfüllt. Es muss immer ausgepackt werden.

Dazu gibt es sogar wissenschaftliche Studien. Der Klassiker stammt hier von dem Marketing-Professor Daniel Howard von der Southern Methodist University in Dallas, Texas. Der kam schon 1992 zu dem Ergebnis: Eine schöne Verpackung finden die Beschenkten schön. Sie steigert die Erwartung an den Inhalt und die Dankbarkeit gegenüber dem oder der Schenkenden.

Erfunden haben die Geschenkverpackung aus Papier übrigens die, die auch das Papier erfunden haben: die „alten“ Chinesen vor etwa 2000 Jahren. Bei ihnen findet sich auch ein dritter wichtiger Sinn des Verpackens: Damals ging es um Geldgeschenke. Und es soll ja nicht jeder wissen, was oder wie viel man von wem geschenkt bekommt. Die Tradition hat sich dort bis heute erhalten: Rote Umschläge mit Geldscheinen sind ein fester Teil der chinesischen Kultur.

Das ändert nichts an den 8000 Tonnen Weihnachtsmüll jährlich in Deutschland. Oder den 365.000 Kilometern weggeschmissenen Papiers, die jemand mal für ein normales „Christmas“ in Großbritannien errechnet hat und die so etwa dem Weg zum Mond entsprechen.

Was tun? Wenn Sie Ihre Geschenke verpacken, aber trotzdem Papier sparen wollen, dann müssen Sie jetzt ganz tapfer sein. Denn: Es geht nicht ganz ohne Mathematik. Aber die ist nicht so kompliziert und macht sogar Spaß.

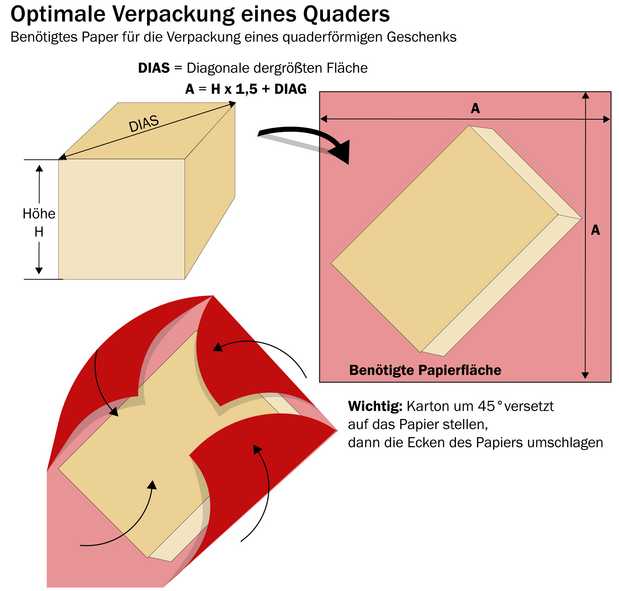
Quader sind die wohl häufigste Form unter dem Weihnachtsbaum. Möchte man einen solchen mit möglichst wenig Papierfläche einpacken, ist es natürlich naheliegend, dessen „Netz“, auch „Abwicklung“ genannt, aufzuzeichnen.

Dieses flache Muster aus sechs Rechtecken kann man ausschneiden, falten, um den Quader herumlegen und die Kanten dann zusammenkleben. Rein praktisch verliert man dabei aber eher Papier, als welches zu sparen. Denn wahrscheinlich wird man viel von dem Abgeschnittenen nicht mehr verwenden können und wegwerfen müssen.

Womit wir bei der eleganten mathematischen Lösung für das Einpacken dieses „dreidimensionalen Polytops“ wären, die solches Geschnippel vermeidet. Sie stammt von der Mathematikerin Sara Santos vom King’s College in London.

Sie hat auch Gleichungen hergeleitet, eine für eine würfelförmige Box und eine für einen Quader. Die ersparen wir Ihnen. Aber wenn Sie wollen, finden Sie sie hier in englischer Sprache.

Die daraus abgeleitete, vereinfachte und den Vorweihnachtsstress sicher reduzierende Version der Methode lautet:

• Nehmen Sie ein Lineal oder einen Zollstock.
• Messen Sie die Höhe der Box und dann auch noch die Diagonale ihrer größten Fläche.
• Multiplizieren Sie die Höhe mit 1,5 und addieren Sie zu diesem Produkt die Länge der Diagonale.
• Das Ergebnis ist die Seitenlänge, auf die Sie das Papier quadratisch zuschneiden müssen.

Also, wenn „h“ die Höhe und „Diag“ die Diagonale der größten Fläche ist und man die benötigte Papierfläche A nennt, dann lautet die vereinfachte Formel:

• A = (1,5 x h + Diag) x (1,5 x h + Diag)

Und wenn man das, was jeweils in den Klammern steht, nicht gleich wieder vergisst, dann sagt einem der Taschenrechner nicht nur die Fläche, sondern jene beiden gleich großen Terme verraten eben auch die beiden – gleichen – Seitenlängen.

Beträgt „h“ beispielsweise 4 Zentimeter und „Diag“ 5 Zentimeter, rechnet man 4 plus die Hälfte von 4 (oder 4 mal 1,5, wie in der Gleichung, aber das ist nicht nur das Gleiche, sondern auch dasselbe). Dabei kommen 6 Zentimeter heraus, und zu denen addiert man 5. Macht 11 Zentimeter. Das Papier sollte also 11 mal 11 Zentimeter messen.

© Tagesspiegel/Rita Boettcher

Das funktioniert ganz gut für alle Quader, die nicht gerade extrem aussehen, also nicht etwa superflach oder sehr lang sind. Am zuverlässigsten funktioniert es natürlich für eine würfelförmige Box. Die ist ohnehin ideal, denn sie verlangt nicht nur fürs Papier drumherum, sondern auch für die Pappe selbst, relativ zum Raumangebot das wenigste Material.

Der Mathematiker Michael Joswig von der TU Berlin sagt, es gehe hier eigentlich darum, „ein ausreichend großes quadratisches Blatt Geschenkpapier zu haben, um einen Quader einzupacken“. Je mehr der Quader also von seiner Idealform des Würfels abweicht, desto mehr überstehendes Papier gibt es.

Wichtig für die Praxis noch: Die Box darf man dann auf keinen Fall mit den Kanten parallel zum Papier auf dieses stellen, sondern um 45 Grad versetzt. Und dann muss man sehr genau falten, vor allem dann, wenn man etwa bei gestreiftem Papier ein die ganze Box umfassendes Muster hinbekommen will. Denn das ist der andere Vorteil der Methode der Mathematikerin Santos: Wenn man es richtig macht, gehen die Streifen exakt deckungsgleich und gerade ineinander über.

Und man benötigt natürlich Klebeband. Aber das ist ohne Verpackungsmathematik auch nicht anders.

Wenn die Grundfläche nicht quadratisch ist, muss man den erwähnten Papierüberstand aber nicht einfach so hinnehmen, sondern man kann mit ein wenig mehr Mathematik dagegen angehen. Denn der Winkel für den geringsten Papierverbrauch werde dann von jenen 45 Grad abweichen, sagt Joswig. Diese „optimale Rotation“ ausrechnen zu können, könne man aber bereits von Mathe-Studierenden im ersten Semester erwarten.

Von uns hier aber sicher nicht.

Deshalb jetzt zu einer anderen wichtigen weihnachtlichen Formenklasse: dem Zylinder.

Loriot lässt grüßen

Möchten Sie etwas Zylinderförmiges verschenken? Eine Rolle Kekse zum Beispiel oder Smarties oder einen in einer seltsamen Pappröhre mit Deckel ausgelieferten Whisky? Oder in memoriam Loriot vielleicht auch einen Kernbrennstab?

Dann brauchen Sie das, was man für alle Berechnungen mit kreisförmigem Anteil benötigt: die Kreiszahl Pi. Die lautet, in Annäherung, 3,14. Aber nehmen Sie besser 3,15. Denn Pi ist etwas größer als 3,14, was dann bei beschnittenem Papier natürlich bedeuten würde, dass es ein winziges bisschen zu klein geriete, wenn man nur mit 3,14 rechnet.

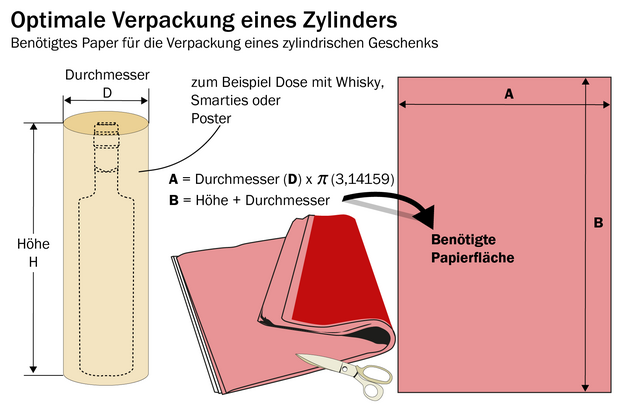
Will man den Zylinder komplett mit Papier umschließen, muss man Pi mit dessen Durchmesser multiplizieren. Das ist dann schon die eine Seitenlänge des zuzuschneidenden Geschenkpapiers. Die andere errechnet sich aus der Höhe des Zylinders plus Durchmesser. Ein bisschen Papierüberschuss bleibt beim Einfalten an den Rändern dann aber natürlich trotzdem.

© Tagesspiegel/Rita Boettcher

Womit wir beim Grundproblem von Gegenständen mit Rundungen wären: Möchte man sie mit einem einzelnen Stück Papier einpacken, so gut und komplex es auch zugeschnitten sein mag, wird es doch nie so funktionieren, dass das Papier komplett anliegt und keinerlei Knitterstellen oder dergleichen bleiben. Bei obigem Quader zum Beispiel ist dies ja durchaus möglich. Bei einem Ball, einer Flasche, einem Blumentopf aber nicht. Das hat auch etwas mit Pi zu tun, der Kreiszahl, die ja hinter dem Komma niemals aufhört, wie wir wissen.

Weil nun aber sphärische Dinge oft verschenkt werden, von Mozartkugeln über Fuß- bis zu Medizinbällen, dürfen sie hier nicht fehlen. Michael Joswig hat für den Tagesspiegel drei Beispiele errechnet, wie man sich dem minimalen Papierverbrauch langsam annähern kann:

Abgestumpfte Verpackungen

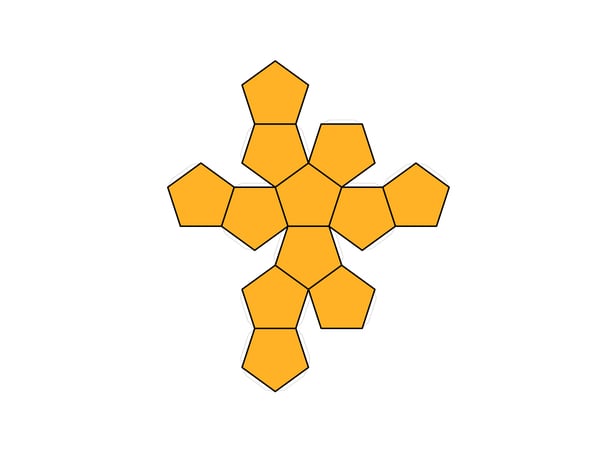
Den Anfang macht ein normales Dodekaeder. Das besteht aus zwölf Fünfecken, deren Kanten sich jeweils berühren. Bei ihm bleibt schon deutlich weniger Luft zwischen Ball und Verpackung – und damit weniger Gesamtfläche Geschenkpapier, als wenn man ein Würfel-Schnittmuster verwenden würde. „Der Ball berührt jeweils den Mittelpunkt jedes dieser Fünfecke“, sagt Joswig. In der Theorie natürlich, oder wenn man den Ball im Weltraum einpackt, statt Papier stabile Pappe nimmt. Sonst gibt es Knülleffekte.

Aber wie das oft so ist in der Mathematik: Man entfernt sich gerne von der Praxis, wenn die Theorie immer hübscher und eleganter wird. Denn wenn man ehrlich ist, spart auch so ein Schnittmuster in der Realität weniger Papier, als die reine Nettofläche aussagt. Denn auch hier ist viel von dem, was man wegschneidet, wahrscheinlich dann doch zu schnipselig, als es noch verwenden zu können.

© Michael Joswig

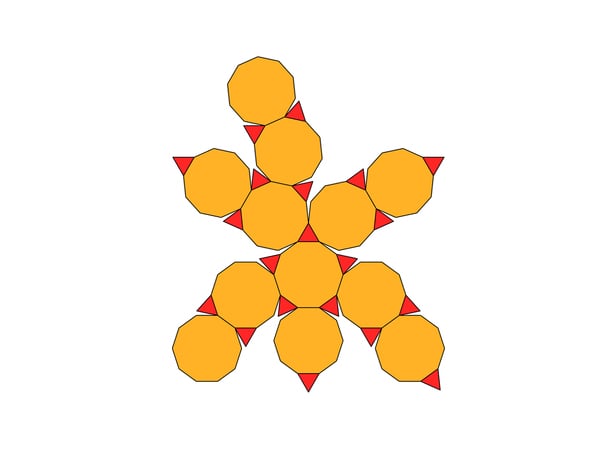
Entsprechend geht es natürlich auch weiter. Noch weniger Papierfläche braucht es, wenn das Dodekaeder zum „Dodekaederstumpf“ wird. „Stumpf“ bedeutet, dass etwas abgeschnitten wird, in diesem Falle jede einzelne Ecke jedes einzelnen Fünfecks des Dodekaeders. So werden aus den Fünfecken Zehnecke. Würde man sie um einen Ball herumlegen, würden allerdings einige dreieckige Lücken bleiben.

Die kann man aber gleichsam mit Papier auffüllen und auch ein entsprechendes zusammenhängendes Schnittmuster für einen einzelnen Bogen erstellen. In der Praxis mit der Schere ist das natürlich anspruchsvoll. Und nach wie vor berührt der Ball hier nur die Mittelpunkte der Zehnecke, nicht aber die der Dreiecke. Das ist nicht optimal, sondern eine Platz- und Papierreserve, an die man noch einmal ran muss.

© Michael Joswig

Korrigieren lässt sich dieser unnötige Platzüberschuss, „wenn man nun die Ebenen, in denen die Dreiecke liegen, an die Kugel heranschiebt, bis sie sie berühren“, sagt Joswig. Er nennt das Gebilde, das dabei herauskommt, einen „tief abgeschnittenen“ Dodekaederstumpf. Der sieht ein wenig aus wie ein klassischer genähter Fußball aus Fünf- und Sechsecken. „Allerdings sind die Sechsecke, die aus den hereingeschobenen Dreiecken entstanden sind, nicht ganz regelmäßig“, sagt Joswig.

Sechsecke, Fünfecke... und Dreiecke

Wie sich hier mit jedem Schritt die nötige Papierfläche verkleinert, zeigt sich, wenn man die Volumina, die jedes dieser Schnittmuster umschließt, berechnet. Bei einem Ball mit einem Radius von einem Meter ergäben sich:

• beim Dodekaeder 5,55 Kubikmeter,
• beim Dodekaederstumpf 5,51 Kubikmeter,
• und beim „tief abgeschnittenen“ Dodekaederstumpf 4,62 Kubikmeter.

Den im Vergleich zum ersten Schritt recht großen Volumengewinn beim Übergang zwischen Stumpf und „tief abgeschnittenem“ Stumpf erklärt der Mathematikprofessor mit nachvollziehbaren, ganz formelfreien Worten: „Die kleinen Dreiecke liegen eben weit weg vom Ball.“

Dieser Ball selbst hat 4,19 Kubikmeter Volumen.

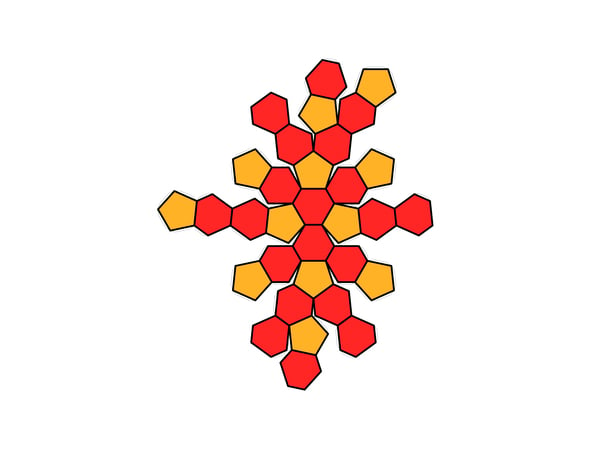
© Michael Joswig

Es bleibt also nach wie vor eine Papierreserve. Die könnte man mit weiteren ähnlichen Schritten aber immer weiter verkleinern: mit komplizierteren Schnittmustern und immer mehr Vielecken, aus denen sich diese zusammensetzen würden.

Andere Mathematiker haben für Kugeln Lösungen errechnet, bei denen etwa Schnittmuster herauskommen, die aus vielen bauchig-lanzettförmigen Lamellen bestehen. Deren Spitzen laufen an den beiden „Polen“ des Balls oder der Kugel zusammen. Der Nachteil hier ist nicht nur, wie Joswig sagt, dass diese kurvigen Formen noch einmal weit „schwieriger herzustellen wären“, sondern auch, dass die Lanzetten sich für maximale Papierersparnis an jenen Polen an Punkten mit der Ausdehnung Null treffen müssen. Sie sind dann also eigentlich Einzelkomponenten und können nicht Teil eines zusammenhängenden ausgeschnittenen Bogens sein.

Wenn man selbst wirklich Papier sparen will, könnte man sich aber überlegen, vielleicht einen nicht ganz so großen Ball zu verschenken. Oder doch das Papier ganz wegzulassen? Rein theoretisch wäre das eine Überlegung wert.

Eine andere Möglichkeit des Kugelpackens, vorgestellt von Mathematikern aus Belgien im Fachmagazin „Computational Geometry“, sind speziell berechnete dreieckige Papier- oder Folienstücke. Die ließen sich auch massenhaft ausstanzen oder zuschneiden und würden sich etwa für einzeln verpackte Mozartkugeln und Ähnliches eignen.

Natürlich gibt es Berechnungen auch für alle möglichen anderen Formen. Wer etwa ein Modell eines Pharaonengrabes oder einzelne Stücke Toblerone verschenken will, muss sich ein Schnittmuster für eine Pyramide errechnen. Wer ein Dreirad materialsparend einpacken möchte, sollte es in einen 3D-Scanner stellen und hoffen, dass ein spezielles Computerprogramm dann ein Schnittmuster ausspuckt. Solche Programme, auch Open Source, gibt es jedenfalls, etwa unter polymake.org.

Taillen benötigen kein Korsett

Allerdings kann es manchmal auch sein, dass es, wenn man Material sparen will, gar nicht sinnvoll ist, das Objekt komplett nah an seinen Oberflächen zu verpacken. Für ein Dreirad etwa könnte das bereits zutreffen. Für alles, was konkav ist, gilt es in jedem Fall, etwa für eine taillierte Vase. Die umschließt man vielleicht mit einem Quader mit zwei Seitenlängen, die dem größten Durchmesser der Vase entsprechen, und einer dritten Seitenlänge, die gleich der Höhe ist. Oder noch besser natürlich nach dem Vorbild des Zylinders oben, wobei man den größten Durchmesser der Vase als Zylinderdurchmesser festlegt.

Zum Schluss aber noch etwas für Sie, was wirklich überhaupt nicht berechnend ist und auch keine Verpackung braucht: Frohe Feiertage!